I’ve been describing a project that aims to clarify the unknown paternal ancestry of someone I’m calling “Bob,” using DNA and written records. I identified a likely paternal ancestor and researched descendants of that ancestor to find candidates for Bob’s father.
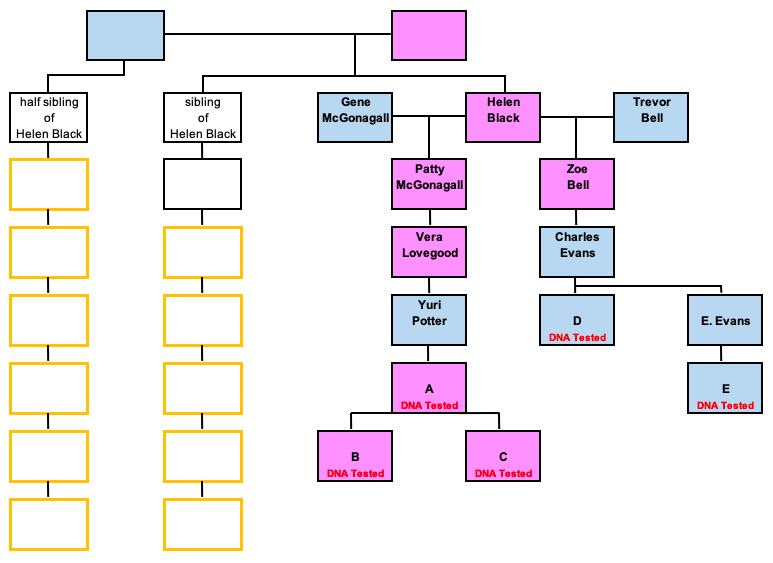
Figure 1 (part of a figure shown in a prior post) shows the tree I’ve constructed for five of Bob’s genetic matches (labeled A through E) back to their common ancestor, Helen Black (note – all names in these posts have been changed). Table 1 shows the amount of shared DNA between Bob and these matches, along with some possible corresponding relationships.


In my efforts so far to build a paternal tree for Bob, I’ve been operating under at least a couple of assumptions:
- The most recent common ancestor (MRCA) of Bob’s genetic matches, Helen Black, is an ancestor of Bob as well (not just his relative). Based on the amount of DNA shared between Bob and his matches, this assumption seemed reasonable, but it was still an assumption.
- Bob’s father was one of Helen Black’s documented descendants, and I have found the documentation of his existence.
Before I went any further, I used the What Are The Odds? Tool (WATO) to take a much more thorough look at the possibilities for Bob’s place in the family tree of these genetic matches.
The WATO Tool allows us to test the probabilities of family structures, accounting for the amount of DNA shared with multiple matches, and we can then compare the probabilities of different hypotheses. Leah Larkin, “The DNA Geek” has a great series of blog posts discussing using probabilities to compare the likelihoods of different relationships, including an introduction to WATO.
In coming up with hypothetical family structures to test, I tried to avoid making further unnecessary assumptions, so I kept the following in mind:
- Don’t assume parents were of an average age when their children were born. Instead of assuming that all generations in the tree were separated by about 20 or 25 years, I tested hypothetical family structures that would result from a range of parental ages. For example, if every ancestor in a line was 18 years old when their child was born, there could be many more generations between Bob and an ancestor than if every female ancestor had been 40 and every male ancestor had been 70 at their child’s birth.
- Small or moderate amounts of DNA shared could result from different relationships. Rather than guessing which branches of the tree seemed more or less likely to be Bob’s line of descent based eyeballing shared DNA, I tested many possible hypotheses and let the statistics rule in or out likely scenarios.
A number of Bob’s genetic matches appear to descend from Helen Black. To see if my assumption was correct that Bob also descended from Helen, I first tested the possibility that Bob, instead, descended from one of Helen’s siblings. Figure 2 shows some of the hypothetical placements for Bob in the family that were tested to address this.

In my analysis, I tried to test any theoretically possible relationship, regardless of the documented children in each line. Evaluating evidence from documentary sources is critical for drawing final conclusions, but at this point, I want to see what lines of descent are statistically possible or likely, and which (if any) could be reasonably ruled out based on amounts of shared DNA. Therefore, as shown in Figure 2, when testing if Bob could have descended from a half sibling of Helen’s, I included the possibility that Helen could have been Bob’s half aunt. This seems unlikely, since Helen was apparently about 115 years older than Bob, but it still could have been possible. Documents suggest that Helen’s parents were both about 20 years old when Helen was born. If Helen’s father had a son when he was 70, Helen would have had a half brother 50 years her junior. If that half brother had a child late in life, the half brother could have, theoretically, been Bob’s father. A full sibling, on the other hand, could not have been this much younger than Helen (her mother would not have given birth at age 70); Bob’s father could have been Helen’s half brother, but not her full brother. Conversely, if everyone in the line of descent became a parent at about age 18, many more generations would have passed between Helen Black’s generation and when Bob was born.
When the likelihood of each of these theoretical relationships was tested with WATO, accounting for the amount of DNA shared with these matches, each test was given a score of 0, indicating that the hypothesis was “Not statistically possible with the amounts and tree as entered” (see Figure 3). So those lines of descent were ruled out (at least unless some additional piece of evidence convincingly points otherwise).

Similar tests were repeated to test descendants (at various levels) of Helen Black, Patty McGonagall, Zoe Bell, Vera Lovegood, and Charles Evans. Since this involved a lot of tests, I’ve described it in detail in a supplemental post. The result of all possibilities tested is shown in Figure 4.

Placement was tested for Bob at various places throughout the Helen Black family tree, and only a handful of situations were deemed statistically possible. The most likely of these suggested that Bob’s father was either a son or a grandson of Patty (McGonagall) Lovegood.
Conveniently, this matches nicely with the evidence I found previously, showing that:
- While most of Helen Black’s descendants lived and died in the Southern U.S., two sons of Oscar and Patty (McGonagall) Lovegood moved to the Midwestern state where Bob was born (see Part 5).
- A Y-DNA test suggests that Bob’s paternal surname may likely be Lovegood (see Part 5).
While in this case, a more thorough analysis of autosomal DNA results led me to roughly the same conclusions as I had gotten to without it, I feel a lot more confident that I’m on the right track after going through this process. And if I hadn’t had the geographical clues to narrow down the possible candidates in this family, an analysis such as this could have been even more helpful.
This technique could also be used to help find the place of an unknown match within a family tree. Placing a match may be a bit more difficult, though, than placing a tester whose results you manage; in order to place a match among known relatives, you need to know how much DNA that match shares with those known relatives. This is only possible with some testing companies and GEDmatch (without the cooperation of these known relatives). For your own test results (or those you manage), it is more straightforward to determine the amount of DNA shared with matches with any of the major DNA testing companies.
All Posts in the Series:
- DNA & A Question of Paternity: Part 1 – Introduction
- DNA & A Question of Paternity: Part 2 – Starting with what we knew
- DNA & A Question of Paternity: Part 3 – Identifying Autosomal Matches
- DNA & A Question of Paternity: Part 4 – Building a New Family Tree
- DNA & A Question of Paternity: Part 5 – Bringing together Autosomal & Y-DNA Results
- DNA & A Question of Paternity: Part 6 – Statistically testing hypothetical relationships
- DNA & A Question of Paternity: Part 7 – Bringing the evidence together
- DNA & A Question of Paternity: Part 8 – Analysis with a new match